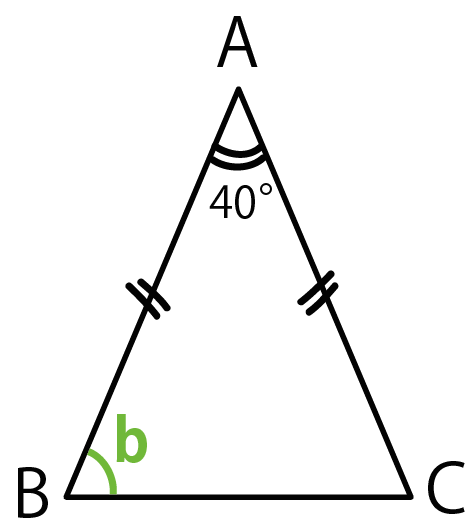
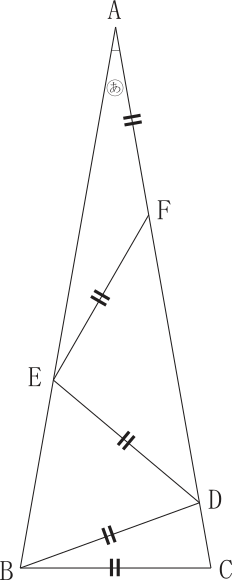
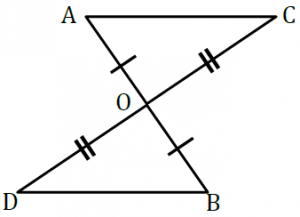
三角形の内角の和(180°) (角b角c) で計算すると、 180 (6565) = 50° になるね! まとめ:二等辺三角形の角度の求め方は2つの公式で一発! 2等辺三角形の角度の問題は、 頂角から底角を求める;1次 の三角形の名前を答えなさい。 (1) 3本の辺の長さが2cm,5cm,5cmの三角形 答え (2) 3本の辺の長さが4cm,4cm,4cmの三角形 答え 2次の三角形のうち、正三角形には 、二等辺三角形には 、どちらでもない三角形 さ 2cm,三角形abcと三角形dcbは合同です。 三角形abcは二等辺三角形なので,辺abと辺 acの長さが等しくなります。さらに,角baeと 角cafが等しく,角abeと角acfが等しいため, 一辺とその両端の角度が等しいので,三角形abe と三角形aceは合同です。 65° 79° a b e f c 38° 34° 41° 31° a b c b c e
コンパスと定規を使った正三角形の描き方 図形の描き方011a 夏貸文庫
二等辺三角形 書き方 角度
二等辺三角形 書き方 角度- 二等辺三角形の性質の中に、 二等辺三角形の頂角の二等分線は底辺を垂直に2等分する ってやつがあったはずだ。 こいつを使ってやると、 二等分線ahはbcの垂直二等分線 になっているはず。 つまり、 ah ⊥ bc;・二等辺三角形では、3つの角度のうち1つが分かれば残りの角度も計算できます。 ・計算には、 頂角 + 底角 + 底角 =180° という関係を使います。 ・(おまけ) 下の図のように二等辺三角形の向きが変わっても、頂角と底角を間違えないようにしましょう。



コンパスと定規を使った正三角形の描き方 図形の描き方011a 夏貸文庫
右図1の三角形 abc が ab=ac の二等辺三角形ならば ∠ abc= ∠ acb が成り立ちます. この性質と三角形の内角の和が 180 °になるという性質を使うと,二等辺三角形の3つの角のうち1つの角が分かれば,残りの角が求められます.正二十角形は定規とコンパスによる作図が可能な図形である。 下図にて書き方を解説している 作図法 「半径2の正円」(緑)と「辺の長さが1とφの黄金長方形」(橙)を活用すると図のように当該正円の円周を等分する点を求めることができる。 脚注 脚注の使い方 関連項目 外部リンク 辺の長さが4cm,6cm,6cmの二等辺三角形のかき方を考えましょう。 指示1: 二等辺三角形に指を置きなさい。 おとなりと確認。 ・ストローのではなく,下の完成形に指を置く。 指示2: その二等辺三角形の左上に④と書きなさい。 その左,二等辺三角形
証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説! 正三角形の角度 正方形、ひし形との融合問題を解説!←今回の記事正三角形や二等辺三角形を作図する場面では,図はかけているものの,補助線を残して正確に 作図できていない児童が多かった。本単元でも作図の場面があり,補助線を残しておくことや測 った辺や角の大きさは必ず記入することはノート指導の基本として徹底したい。また,角度を組 み合わ こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記事
・ 二等辺三角形、正三角 形の概念、性質、かき 方 ・ 形としての角の概念、 大小比較 第3学年「長方形と正方形」 ・ 直角の概念 ・ 平面図形を構成する 要素(辺・頂点) ・ 長方形、正方形、直角 三角形の概念 -2- 調査の結果は、以下の通りである。 (7月16日 28/30名実施) 前 提 内 容二等辺三角形が見つかったら どこが頂角で底角なのかをしっかりと把握することができれば 角度の問題は楽勝なはずです。 たくさんの問題演習を通して 理解を深めていきましょう! ファイトだー(/・ω・)/ 二等辺三角形をマスターしたら 次は正三角形ですね!角度を単位円上の点として扱う幾何代数の技法によって、二等辺三角形の性質を確認します。 ※ わざわざ簡単なことを難しく説明するようですが、基本的な事項を幾何代数の技法ではどのように扱うのかを確認するのが目的です。 クリフォード代数は



測点 2点透視 パースフリークス




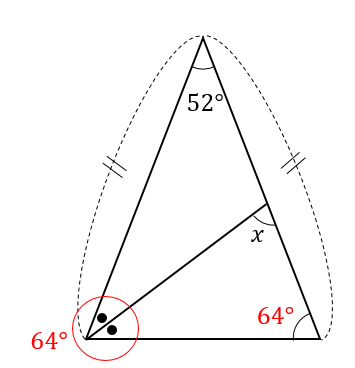
二等辺三角形の頂角の角度を求めよ 解答編その1 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
教え方4 円を使った二等辺三角形と正三角形のかき方を考えさせます。 下の図を見せて、考えを言わせます。 円周上のどこの2点を使っても 円の中心と結ぶと 二等辺三角形になることを教えます。 参考・・・コンパスの使い方二等辺三角形の4つの性質と4つの条件 二等辺三角形の角度の求め方と例題 対頂角、同位角、錯角の意味を分かりやすく解説 四角形の内角の和が360°であることの2通りの証明 多角形の内角の和の公式を3通りの方法で証明する 正多角形の内角と外角の大きな,拡 大したcad表 示画面上で行える,新 たな四則演算方 法を導入したそ して,二 等辺三角形の辺の長さと角度の二 等分線長さとの関係を近似式の形で与えた cad表 示画面上の作図の精度は,二 等辺三角形



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
可能になるのは,第4学年で「角度」の学習をした後になるため,この段階で正三角形になって いることを確かめる場合には,コンパスで長さを測る活動が必要であると考える。 15 343 教材比較「円の半径を使った二等辺三角形や正三角形のかき方」 会社名 教材の内容(1)二等辺三角形や正三角形,図形としての角の大きさについて理解する。 (2)二等辺三角形や正三角形のかき方が分かり,作図できる。 3 指導計画(全11時間) 第一次 5時間 二等辺三角形と正三角形 第二次 3時間 三角形のかき方二等辺三角形,正三角形について知ること。 角について知ること。 本単元は,二等辺三角形と正三角形の定義と一つの頂点から出る二本の辺が作る形を角 とすることを理解することをねらいとしている。本単元では,三角形の辺の長さに着目し て特徴を見出し分類したり,定規やコンパスを



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



正方形と二等辺三角形の問題です 角度xを出し方をお教えください 宜しく Yahoo 知恵袋
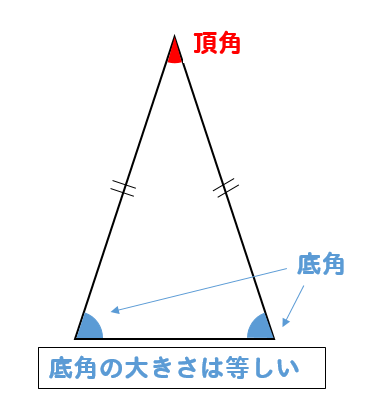
2:二等辺三角形の2つの特徴(角度と辺の長さ) 二等辺三角形の定義がわかったところで、二等辺三角形の特徴について学習していきましょう! 二等辺三角形には2つの特徴があります。 特徴1(角度) 特徴の1つ目は、 二等辺三角形の底角の大きさは等しい ということです。(底辺を挟んでいる角のこと)垂直・平行と四角形 図形のしきつめ 正三角形 二等辺三角形 直角三角形 解説 平行四辺形 解説 台形 解説 垂直 垂直 直方体と 立方体 直方体と立方体 解説 直方体と立方体の展開 解説 がい数 概数スロット 解説 概数スロットv3 解説 計算スロット 解説3 角度 三角形が無いから角の大きさが 求められないな。 点Oと点Cを結ぶと,三角形OAC,OCBは二等辺三角形になる んだ! x O A C B 42° 40° 42° 40° O A C B い あ 18 つま き算数_図形p014_069indd 18 AM



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
二等辺三角形や正三角形で,1つの角の角度を計算で求める方法を教えて 無断複製・転載・翻訳を禁ず GAKKEN B Title ここでは、二等辺三角形の辺の長さ、角度、面積、比の求め方を例題を使って解説していきます。 例題 \(\mathrm{AB} = \mathrm{AC}\)、頂角が \(1^\circ\)、\(\mathrm{BC} = 8\) の二等辺三角形 \(\mathrm{ABC}\) があります。ってことさ。 底辺bc = 8cmだから、 bh = ch = 4 cm だね。
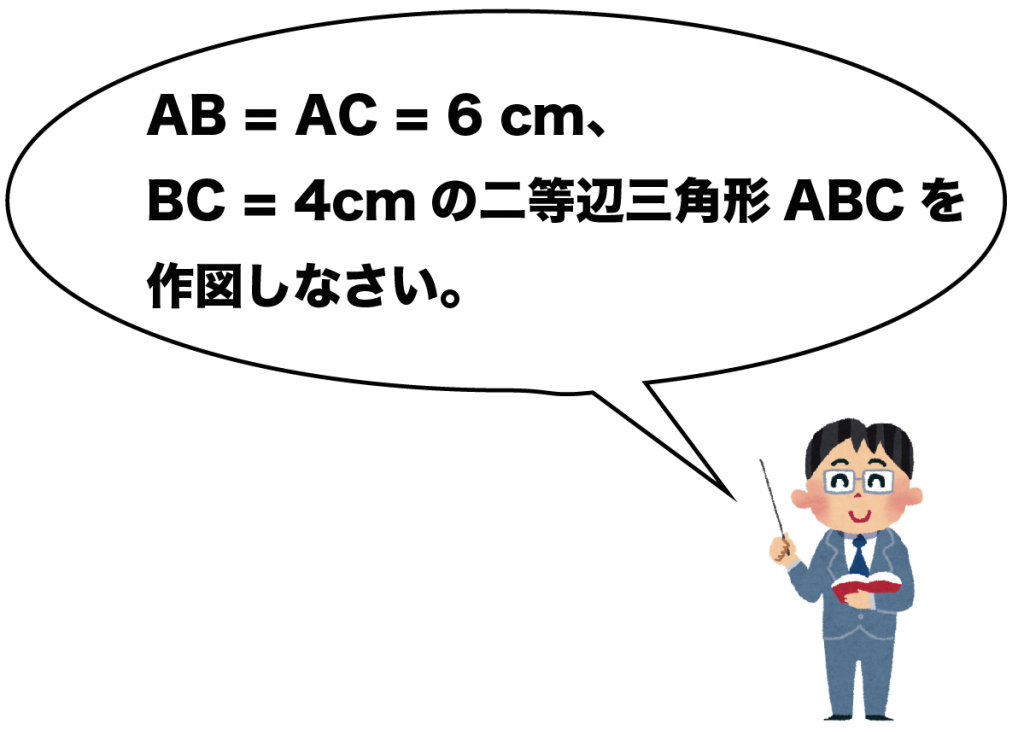



中学数学 二等辺三角形の書き方 作図がわかる3ステップ Qikeru 学びを楽しくわかりやすく
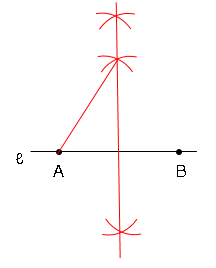



角度の作図の問題 数学の要点まとめ 練習問題一覧
三角形の一辺となる線分と、辺の長さや角度を指定して、三角形の残りの二辺を作成します。 アドインのインストール方法 アドインをインストールする手順は、以下のページをご覧ください。 アドインの使い方 (Ver9 以降の場合) 「三角形」を実行する方法二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ二等辺三角形の角度の求め方(計算) 色々な二等辺三角形の角度を求めましょう。下図をみてください。頂角が90度です。前述した計算式を使います。 α2θ=180 902θ=180 2θ=90 θ=45 頂角が直角の二等辺三角形を、直角二等辺三角形といいます。次の問題です。低角が60度のとき、頂角を



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に
二等辺三角形は,大きさがちがったり,向きがちがってもいいの 3 正三角形とは,どんな三角形なの 4 ものさしとコンパスで,二等辺三角形はどうしてかけばいいの 5 ものさしとコンパスで,正三角形はどうしてかけばいいの 6 三角じょうぎのかどの形は,どのようになっているの(角の意味) 7二等辺三角形の2つの底角は等しいから、 したがって、 ABCは、 が等しい。 ABCは、AB= の二等辺三角形である。 三角形・四角形 定理の逆 1 次のことがらの逆をいいなさい。また、それが正しいときは 、正しくないときは ×をし、その具体例を示しなさい。 257 逆 逆 (3)2つの角が等しい三角形はIf playback doesn't begin shortly, try restarting your device Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典
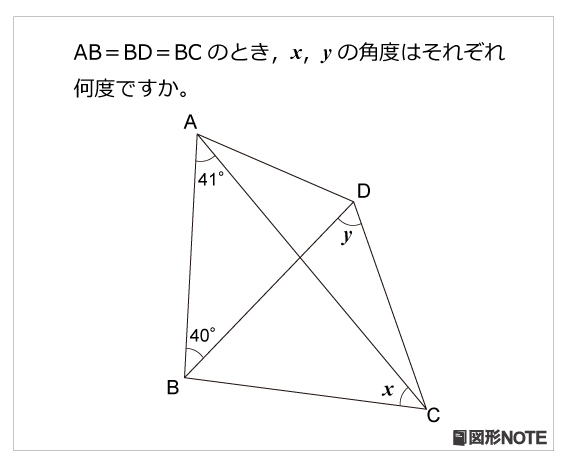



図形noteプレ レベル4 二等辺三角形の発見 算数星人のweb問題集 中学受験算数の問題に挑戦
こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の外心(垂心)」 について、性質の証明や座標の求め方、位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心とは なぜ"外心"なのか、いきなり説明することは困難です。 直角二等辺三角形とは、「 三角形の3つの角度のうち、2つの角度が45°である三角形のこと 」です。 三角形の内角の和は180°ですので、2つの角度が45°ということは、残り1つの角度の大きさは、 180 (4545) = 90°二等辺三角形(にとうへんさんかくけい、英 isosceles triangle )は、三角形の一種で、3 本の辺のうち(少なくとも)2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。
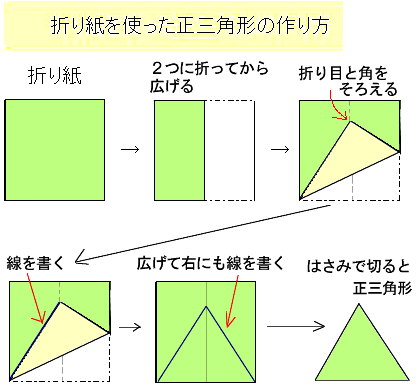



3年算数三角形教え方のポイント
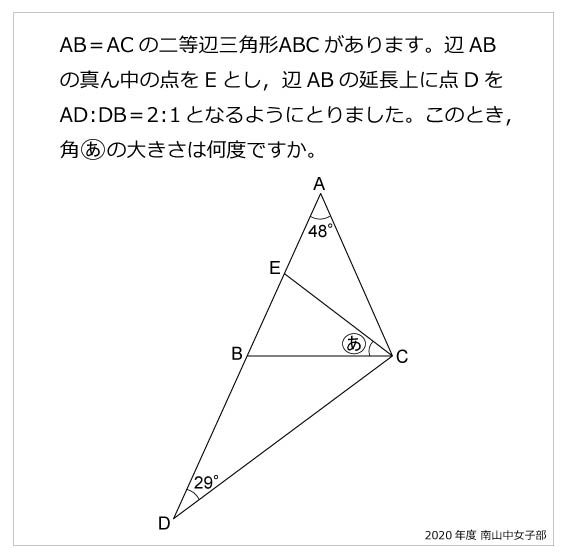



二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
直角二等辺三角形を書く際は、 円の直径に対する円周角が \(90^\circ\) となる 性質を利用します。 斜辺 \(\mathrm{AB}\) を直径とする円の周上に\(\mathrm{AC} = \mathrm{BC}\) となるような点 \(\mathrm{C}\) をとればよいですね。二等辺三角形と正三角形のかき方 三角形の角 しきつめたもよう 面積学習サイト 6平方センチメートルの図形を作ろう 1平方センチメートルの図形を作ろう 円と球 円学習サイト コンパスを使って円をかく コンパスを使って長さをくらべる 小数 1より大きい分数 4年小数学習サイト 1より
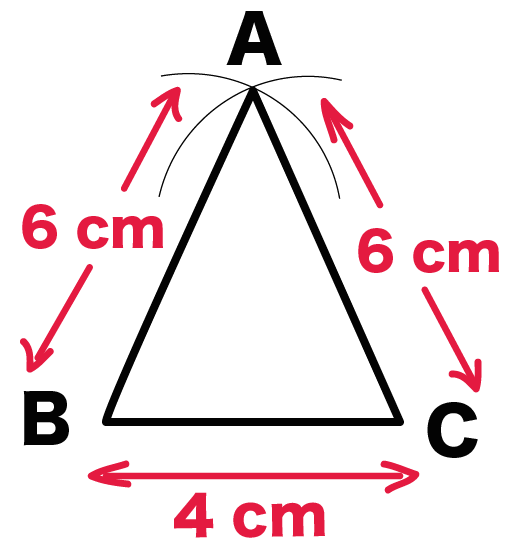



中学数学 二等辺三角形の書き方 作図がわかる3ステップ Qikeru 学びを楽しくわかりやすく




世界一分かりやすい算数 小3 三角形



コンパスと定規を使った正三角形の描き方 図形の描き方011a 夏貸文庫
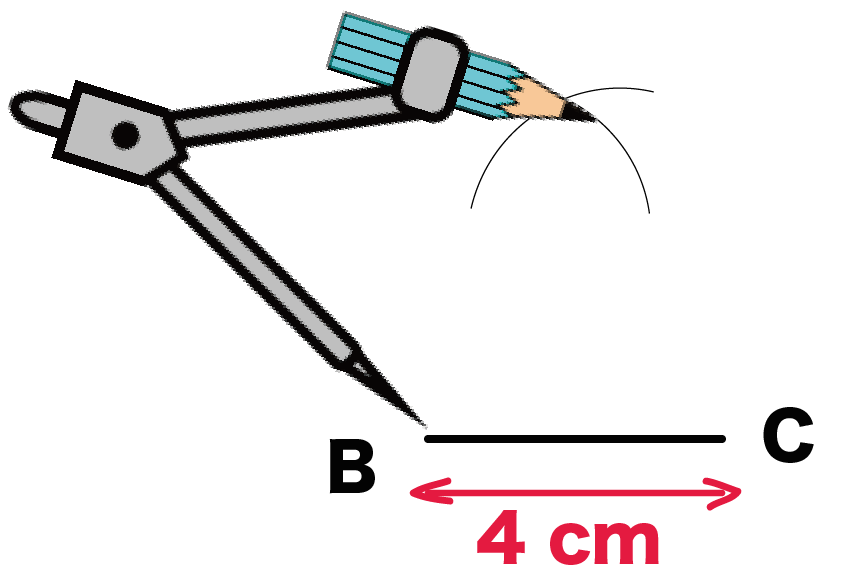



中学数学 二等辺三角形の書き方 作図がわかる3ステップ Qikeru 学びを楽しくわかりやすく
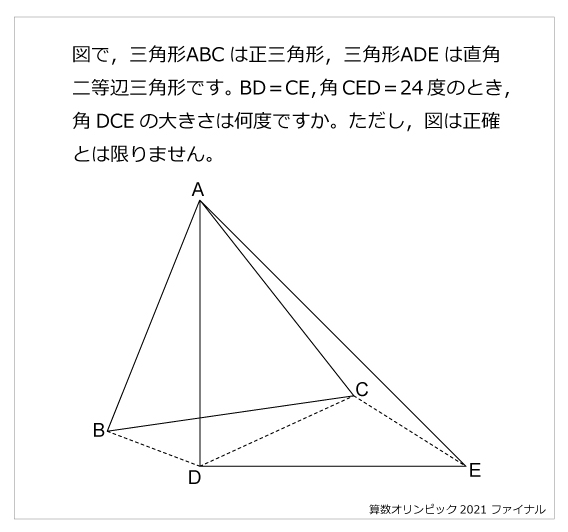



Es0sitebydfbkm



二等辺三角形 In 二等辺三角形 角度の問題 算数の広場




黄金三角形による18 シリーズの三角比 おいしい数学




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



3年算数三角形教え方のポイント




簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath



3



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



1



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




コンパス作図 45度の角度の出し方を解説するよ 中学数学 理科の学習まとめサイト



1



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




すきるまドリル 小学3年生 算数 三角形と角 無料学習プリント すきるまドリル 無料学習プリント




コンパス作図 45度の角度の出し方を解説するよ 中学数学 理科の学習まとめサイト



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




小5 算数 小5 31 三角形の角 Youtube




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



3



幼児教室は ピグマリオン大阪本部 江坂教室 吹田市 英才児養成専門の幼児教室




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




数学 時短演習cote



じょうぎとコンパスで円や三角形をかく 家庭学習レシピ



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
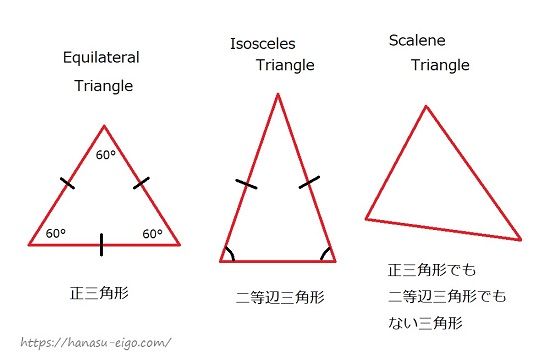



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




二等辺三角形になることの証明 Youtube




三角定規と角度が 150 の三角形の長さと面積を求める Irohabook
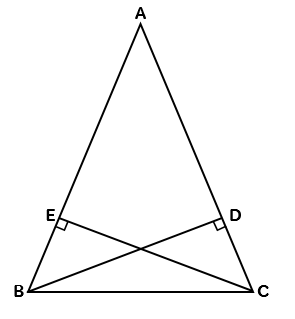



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト
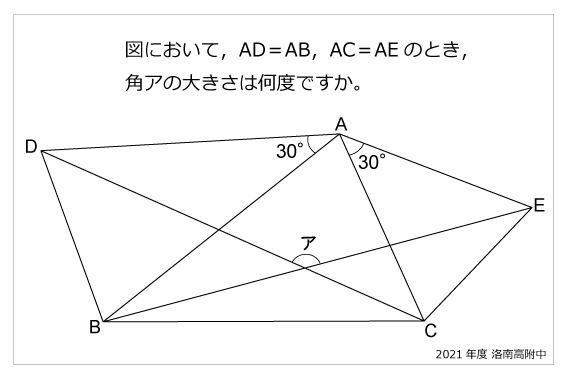



二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦




コンパスと定規で作図 三角形の書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学 中2 64 二等辺三角形 Youtube




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



コンパスと定規を使った正三角形の描き方 図形の描き方011a 夏貸文庫
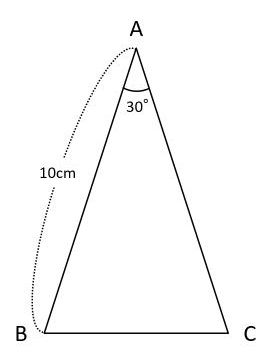



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
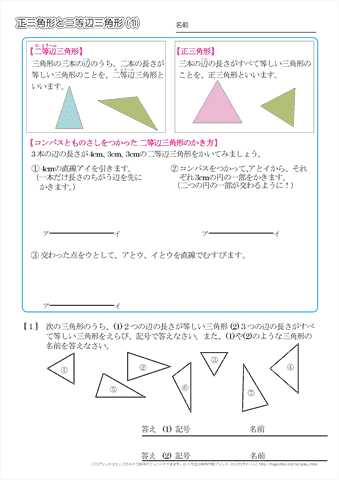



小学3年生の算数 三角形 正三角形や二等辺三角形 練習問題プリント ちびむすドリル 小学生
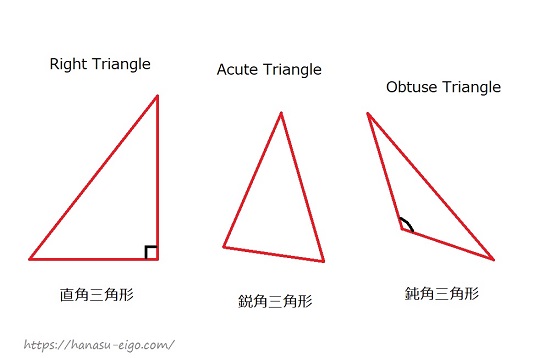



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語
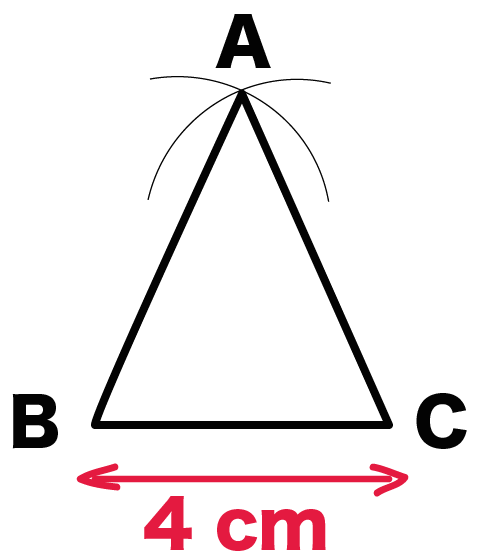



中学数学 二等辺三角形の書き方 作図がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




作図 スクールプレゼンター教材共有サイト スクプレ道場



3年算数三角形教え方のポイント



3年算数三角形教え方のポイント
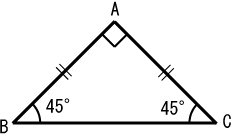



直角二等辺三角形 Wikipedia




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
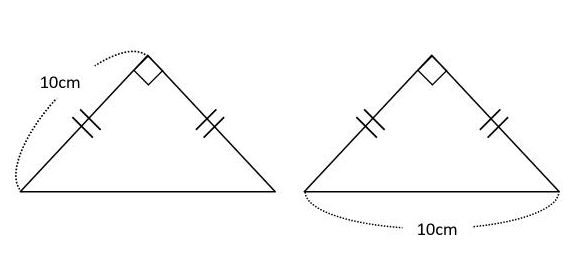



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




小3 算数 小3 42 二等辺三角形と正三角形を書こう Youtube



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



エクセルで三角形を描画するための三角関数再入門 Yamav1 02bのブログ




正三角形や二等辺三角形の内角 Youtube
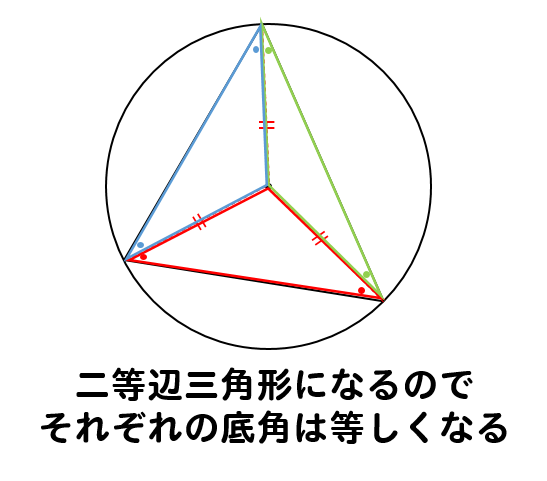



作図 三角形の内接円 外接円のかき方をポイント解説 数スタ




三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




どうやって1本の直定規だけで30度の角度が作れます どうやって1本の直 教えて Goo
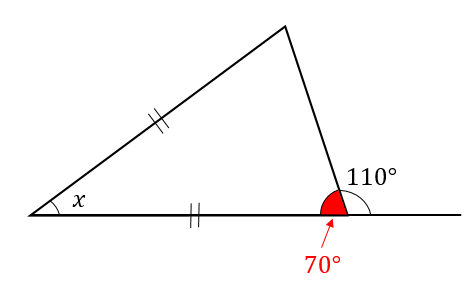



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
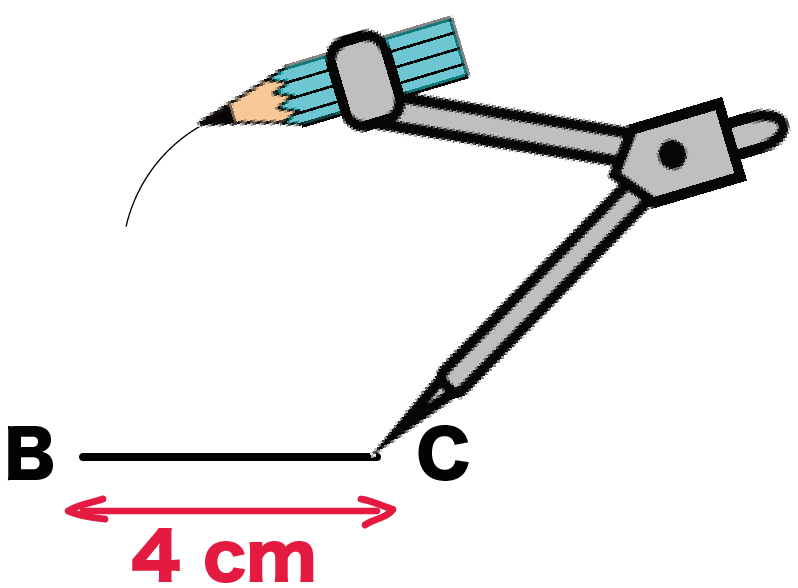



中学数学 二等辺三角形の書き方 作図がわかる3ステップ Qikeru 学びを楽しくわかりやすく
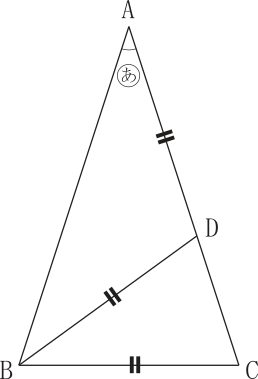



二等辺三角形 In 二等辺三角形 角度の問題 算数の広場




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




角度のコンパスでの作図 中学1年数学 Youtube



2 偶然の角 の一般化にむけて 二等辺三角形から一般の三角形に
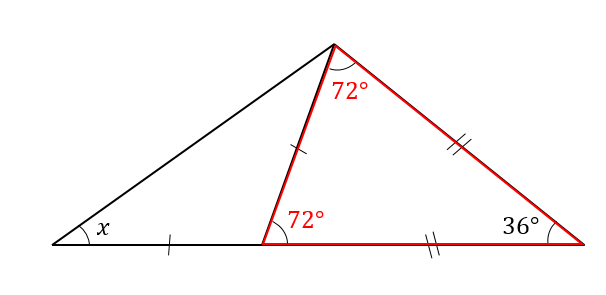



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
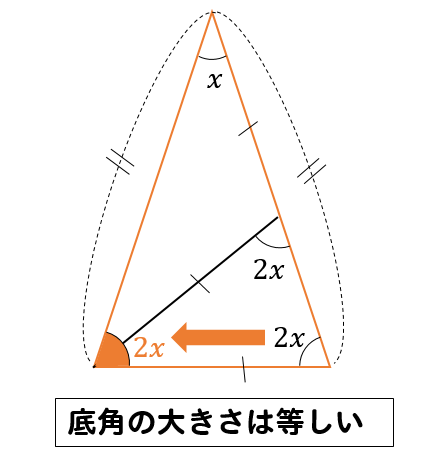



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
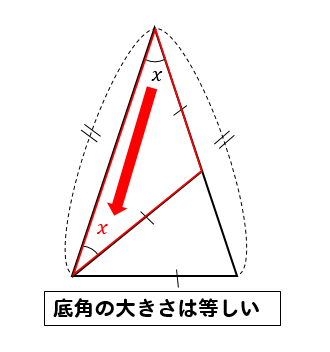



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ
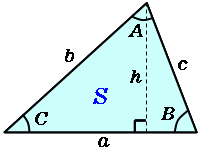



不等辺三角形 高精度計算サイト




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




直角二等辺三角形の書き方教えてください お願いします 直角二等 その他 悩み相談 人生相談 教えて Goo



三角形 Rootpro Cad




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



3年算数三角形教え方のポイント




直角二等辺三角形の書き方教えてください お願いします 直角二等 その他 悩み相談 人生相談 教えて Goo




写真で 私が書いた角度の書き方は違いますか Clear
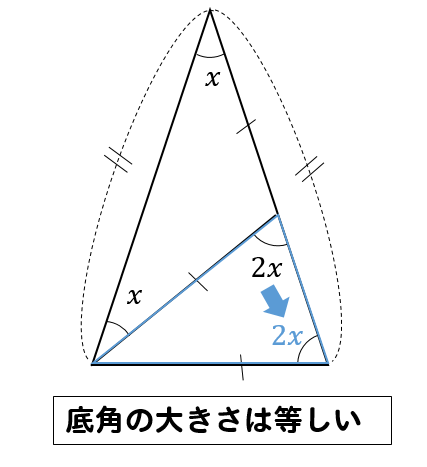



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ



Core Ac Uk Download Pdf Pdf


