こんにちは、ウチダです。 今日は、中学3年生で習う 「三角形の相似条件」 について、まずは図形の相似を解説し、次に三角形の相似条件が $3$ つである理由を明らかにしていきます。 また記事の後半では、狙われやすい証明問題をいくつか用意しましたので、ぜひチャレンジしてみて下さい。 相似な図形の基本事項に関するプリントです。 相似な図形の基本や相似比、相似の記号(∽)などをしっかり確認しておきましょう。 また、相似な図形の長さを比で計算出来るようにすることも大切です。 *プリントは追加する予定です。 16年10基に、図形の相似の意味を理解 する。 相似な2つの 図形を観察し て、相似な図 形の性質を考 えることがで きる。(学習活 動の観察・ノ ート) 相似の意味を 理解してい る。(練習問題 の解決状況の 分析) 2 2.相似な図形の性質を理解す る。 2つの図形
相似な図形の面積比と三角形の辺の比から求める面積比 まぜこぜ情報局
相似な図形の性質
相似な図形の性質- 相似な図形は「同じ形のまま拡大・縮小した図形」なので、対応する角の大きさもそれぞれ等しくなります。 上図を見ると、相似な図形の3つの角の大きさはそれぞれ \(30°\)、\(45°\)、\(105°\) のままで変わっていないことが分かります。〇相似な図形の対応する辺,角,頂点を それぞれ指摘することができる。 〇相似な図形の性質を理解している。 数学的技能 主体性 ・観察 ・プリント ・発表 情 報 収 集 三 解 べ 2 と 角形の 相似 条件を理 し,図形の性質を調 たり,距離や高さを



中学数学単元別 相似な図形 数学 中学校 教材 問題集 305 学林舎 通販 Yahoo ショッピング
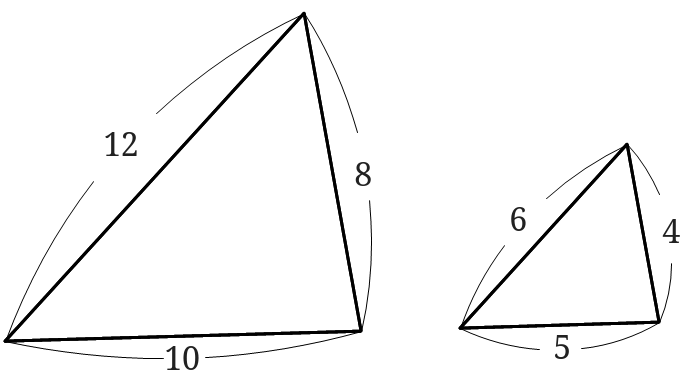
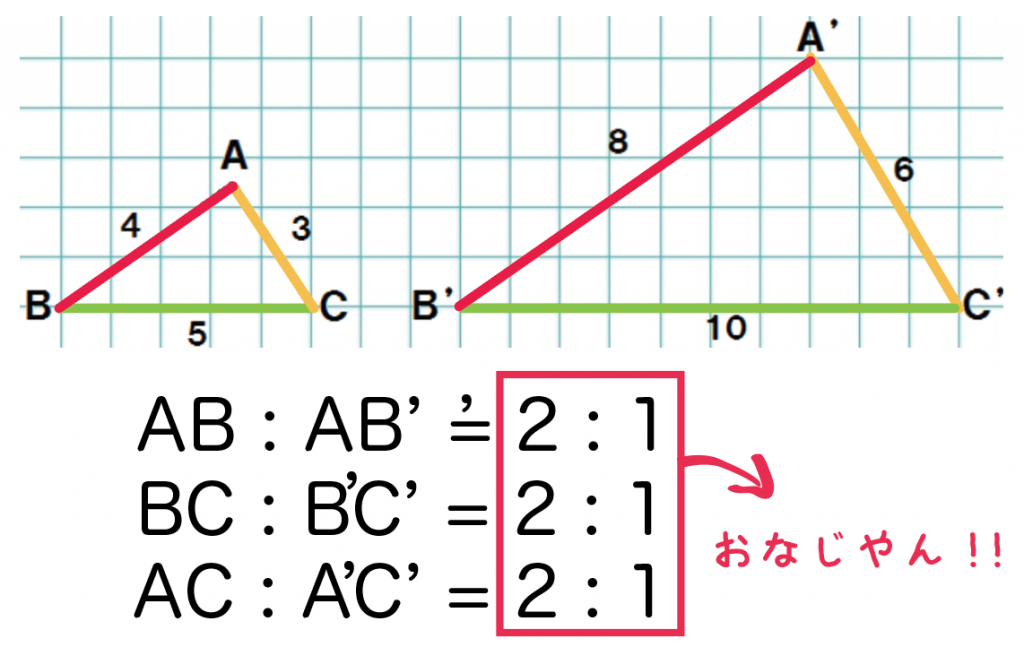
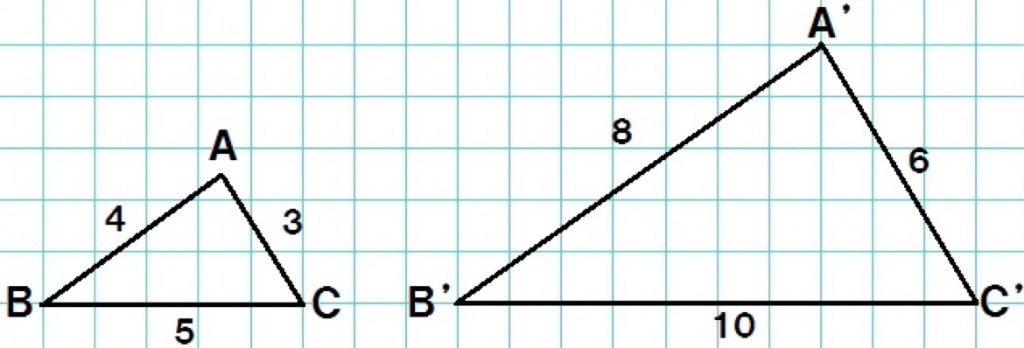
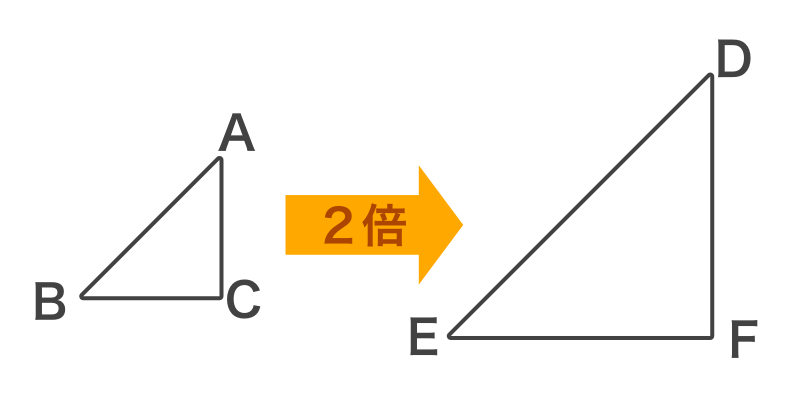
相似な関係にある2つの平面図形の相似比がa:bの場合、面積比はa 2 :b 2 になる という性質があります。 これがおぼえるべき、2つ目の型です。 さきほど示した17種類の内、14個は①と②をベースにしたものです。相似な図形の対応する角は等しいので ∠ade=∠abc 同位角が等しいのでde//bc ① f eを通りabと平行な直線をひき、bcとの交点をfとする。 adeと efcにおいて ab//efで平行線の同位角は等しいから∠dae=∠fec(1) 四角形dbfeは平行四辺形なので db=ef よってaddb=aeecから面積比をだす Step1 相似比を求める まず相似比を出してやろう! 相似比の求め方は覚えてる?? 相似な図形同士の、 対応する辺の長さの比 を求めればよかったね?? 今回でいうと、辺ABに対応する辺は辺A'B'。 AB=3cm, A'B'=6cmだから
中学校3年 相似な図形 21/21時間(東京書籍:新しい数学3 P147 特設) 相似の考えのよさを実感させ,活用しようとする態度を育てよう ねらい ・身近な調理器具にも相似の考えが使われていることを実感することで,日常生活の中自己相似図形とは? 相似縮小変換 f 1 , f 2 に対して, f 1 (D)∪f 2 (D) = D となる図形Dを自己相似図形という。 Dが有界であるものと仮定すれば,Dを描く手続きを次のように作成することで,Dを描くことができる。 Dを描く手続き f 1 (D)を描く f 2 (D)を描く 手続きの終わり相似であることを証明するには「2組」を示せば十分だということ 右図では ∠B=∠Q, ∠C=∠R を示せば, ∠A=∠P は自動的に成り立つ. (2) 「3組の辺の比がそれぞれ等しい」という書き方は2種類ある.
相似の図形では、各辺の相似比はすべて同じです。今回の場合、 ABC∽ AMNの相似比は3:1です。そのため、 一つの辺の長さが分かれば他の辺の長さについても計算できるようになります。 例えば、MNの長さが3cmの場合、MN:BC=1:3のため、BCの長さは9cmです。中学数学 相似な図形の内容 z 相似な図形の性質 z 相似の位置 z 相似比 z比の値 z 三角形の相似条件 z 三角形の相似条件を使った証明 z 相似の利用(測量) z 三角形と比 z 三角形と比の定理の逆 z 中点連結定理 z 平行線と比 z 三角形の角の二等分線と比相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので




スタディピア 図形




相似な図形の面積と体積 の勉強法のわからないを5分で解決 映像授業のtry It トライイット
「相似な図形」のパターンがある? 実は、三角形の相似の問題では、 よく使われる 「基本の形」 が2つあります。 その2つとは 「ちょうちょ型」 と 「ピラミッド型」 です。 これらが見えれば、 "相似形だ!"と分かるのです。 見つけ方のコツ ですね。『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので相似な図形の面積比 相似な図形の面積の比は「相似比の \(2\) 乗の比」になります。 つまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他




図形の相似 Wikipedia



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく
授業実践記録(数学) 1.はじめに 授業の形態や課題を工夫する事で楽しみながら学習できれば,意欲,定着度,思考力, 表現力などを高めていけるのではないかと考えた。 そこで,図形と相似の導入で以下の点に留意しながら授業実践を行った。 尚相似とは ある図形を拡大、縮小した図形は、もとの図形と相似であるといいます。 相似な図形どうしは、まったく同じ形をしているといえます。 例えば下の図の四角形 \(abcd\) と四角形 \(hefg\) は相似数学35章図形と相似「相似な図形」<準備問題①> 組 番 名前 1三角形の合同条件を書きなさい。 2次の図で,AB//CDのとき,次の問いに答えなさい。



5章 相似 タカラゼミ



3年 相似な図形とその性質 数学イメージ動画集 大日本図書
たとえば,右の図形で ab//cd のときは abe と dce は相似図形になり, bece=abdc=aede が成り立つ. だから, bece の比が分かっていれば abdc の比が分かる.・ 相似の概念を明らかにし、2つの相似な図形を観察して、相似な図形の性質を考えること ができる。 ・ 相似の意味、性質、相似比について理解する。例 相似な図形の例 直線, 正三角形, 直角二等辺三角形, 正方形, 正多角形, 円, 放物線, 直角双曲線, 正多面体, 球など これらはそれぞれ、一方を適当な率で拡大または縮小し、適当に平行移動、回転、鏡映を施すと他方に重なる。 このとき双方は形が同じであるが、大きさと向き(平面上では



相似な図形 さわってうごく数学 Aquaアクア Para Android Apk Baixar




明日テストなので至急お願いします 相似な図形の問題で の問題のhf Fcが1 3に Clear
A B C D E 中3年 相似な図形(相似な図形の面積と体積) 学年 組 氏名 1 右の図の ABCにおいて,点D,点Eはそれぞれ辺AB,AC上の点相似な図形の相似比 を求める。 知図形の相似の意 味を理解している。 4 ①相似な 図形 比の性質を用いて,相似な 図形の対応する辺の長さを 求めることができる。 相似な図形の辺の長 さや,各の大きさを求め る。 比の性質とそれを利 用して相似な こんにちはtanukiです。 今回は相似についての記事ですが学習ポイントとかではなく教え方の話です 。 たまに長年算数を教えている先生でも 「相似とは形が同じで大きさがちがう図形の関係のこと」 と説明される方に出会います。 「形も大きさも同じ」合同と比較しての説明なのでしょう。
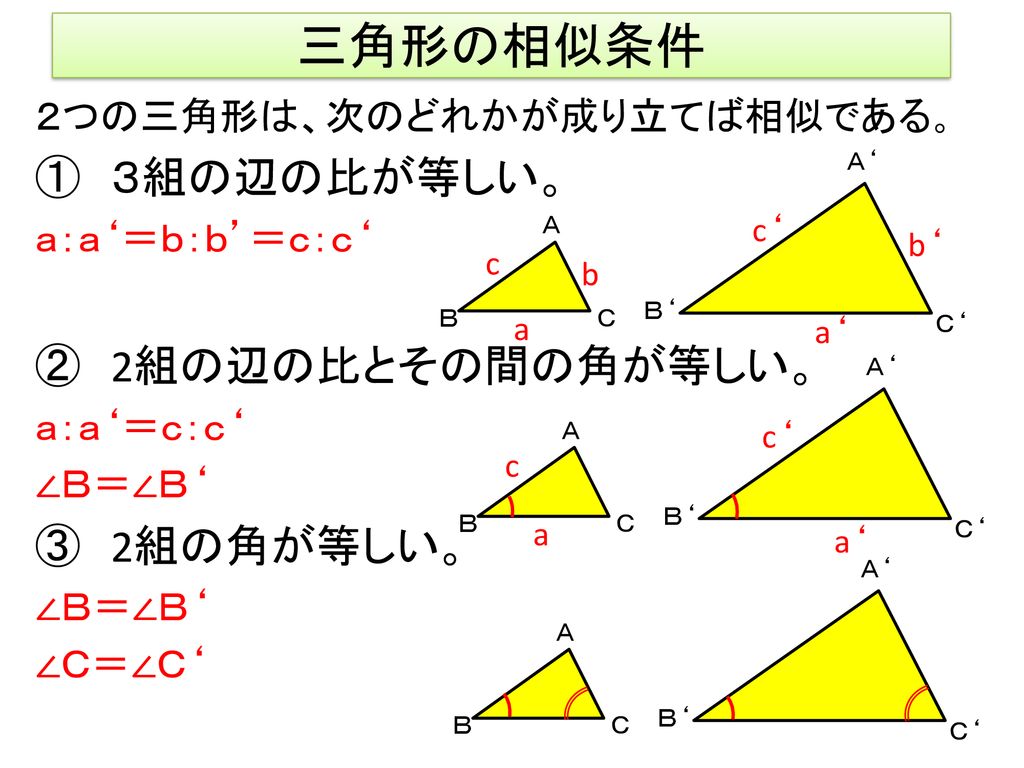



本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download
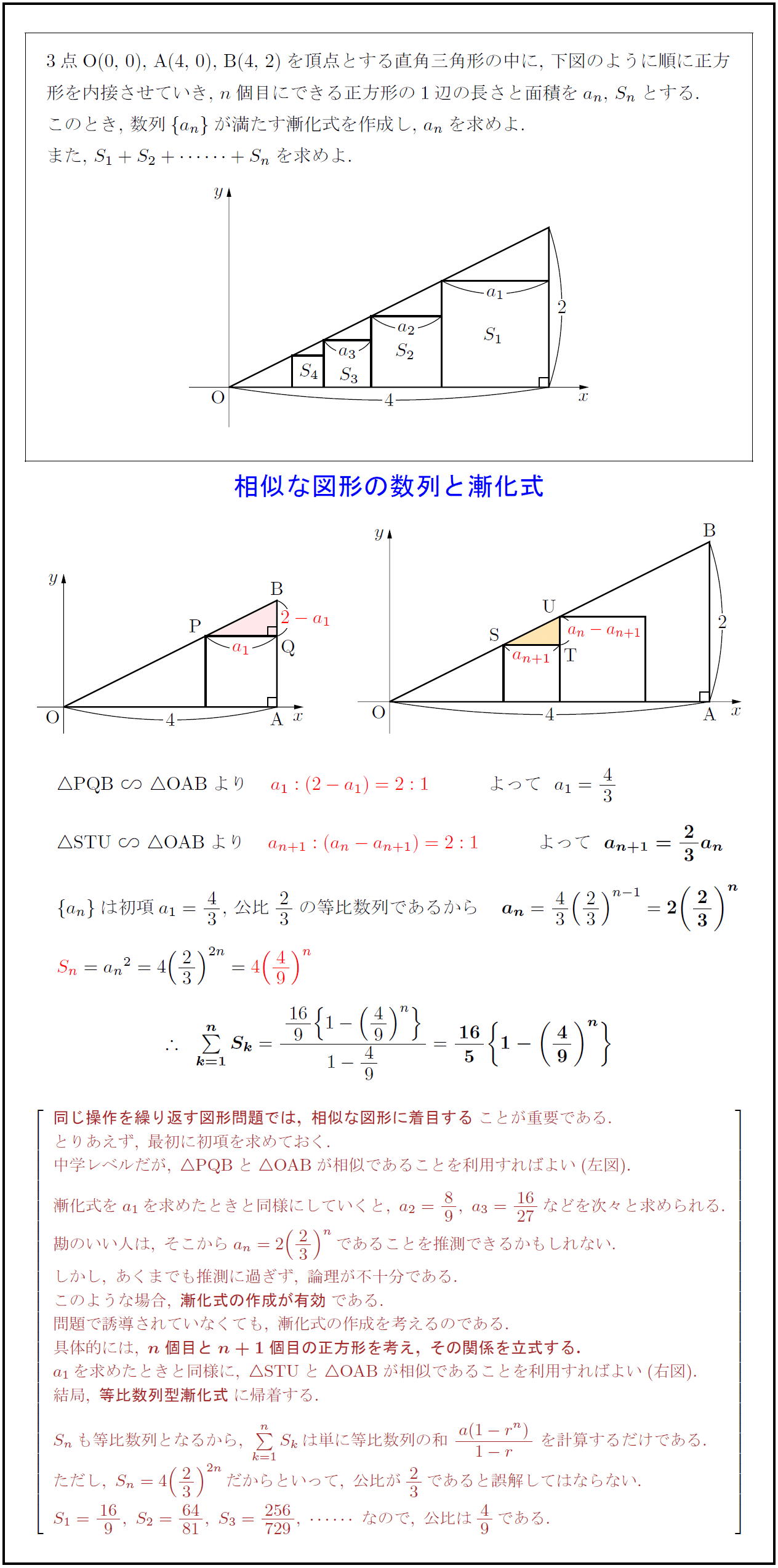



高校数学b 相似な図形の数列と漸化式 受験の月




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ




中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



よっちゃんルーム



3




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




三角形の面積比と相似比 チーム エン




初等数学模索生活 相似な図形 1




三角形の相似条件と証明問題の解き方 数学fun




中学数学 理科 寺子屋塾の復習サイト 相似な図形 総合




相似な図形の面積比と三角形の辺の比から求める面積比 まぜこぜ情報局
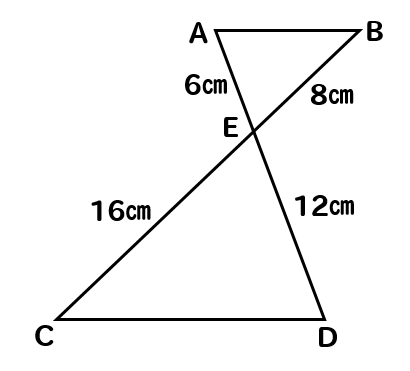



中3数学 相似な図形の見つけ方 相似条件とは 基本問題を使って解説 数スタ



Q Tbn And9gcte8fsqvrlckxdilyd5wnblxavnplfa7mg7ddvhyyrzhuvjel Usqp Cau




5 相似な図形 1




中3数学 図形と相似27 相似な図形の面積比 すべて無料 星組の中学数学講座




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ




相似な図形 しっしーのお計算ん向上委員会



1



中学数学単元別 相似な図形 数学 中学校 教材 問題集 305 学林舎 通販 Yahoo ショッピング
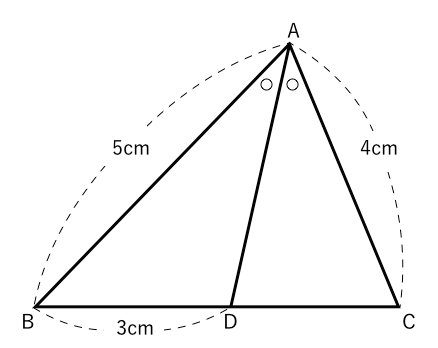



相似な図形 角の二等分があったらこれ 苦手な数学を簡単に




三角形の相似条件




中学数学 図形の相似
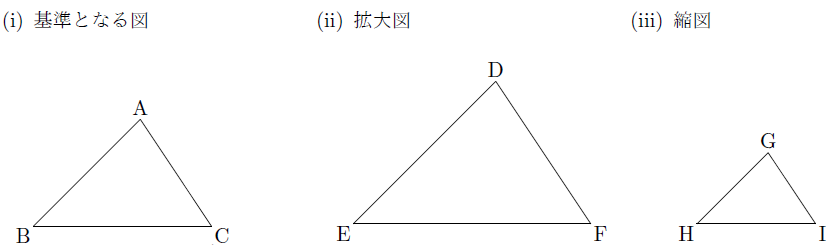



相似な図形 まなびの学園



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典



数学問題の出題範囲詳細



相似比
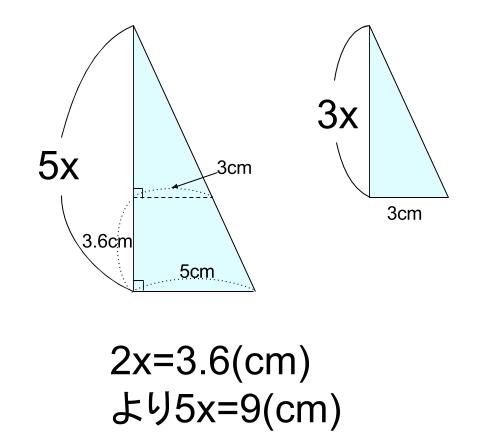



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
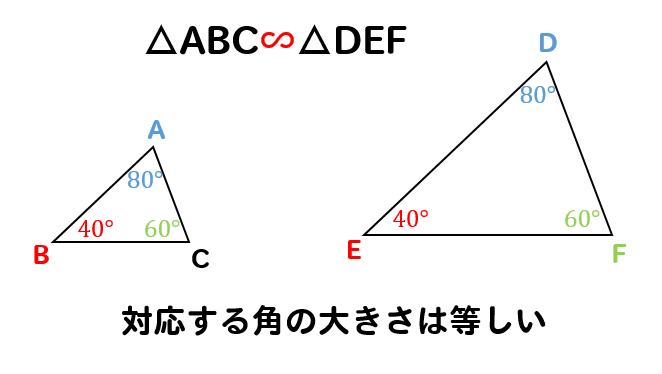



中3数学 相似の基本性質をわかりやすく問題解説 数スタ




相似な図形 図添付忘れ 図で abcと adeは相似な三角形で ap Okwave
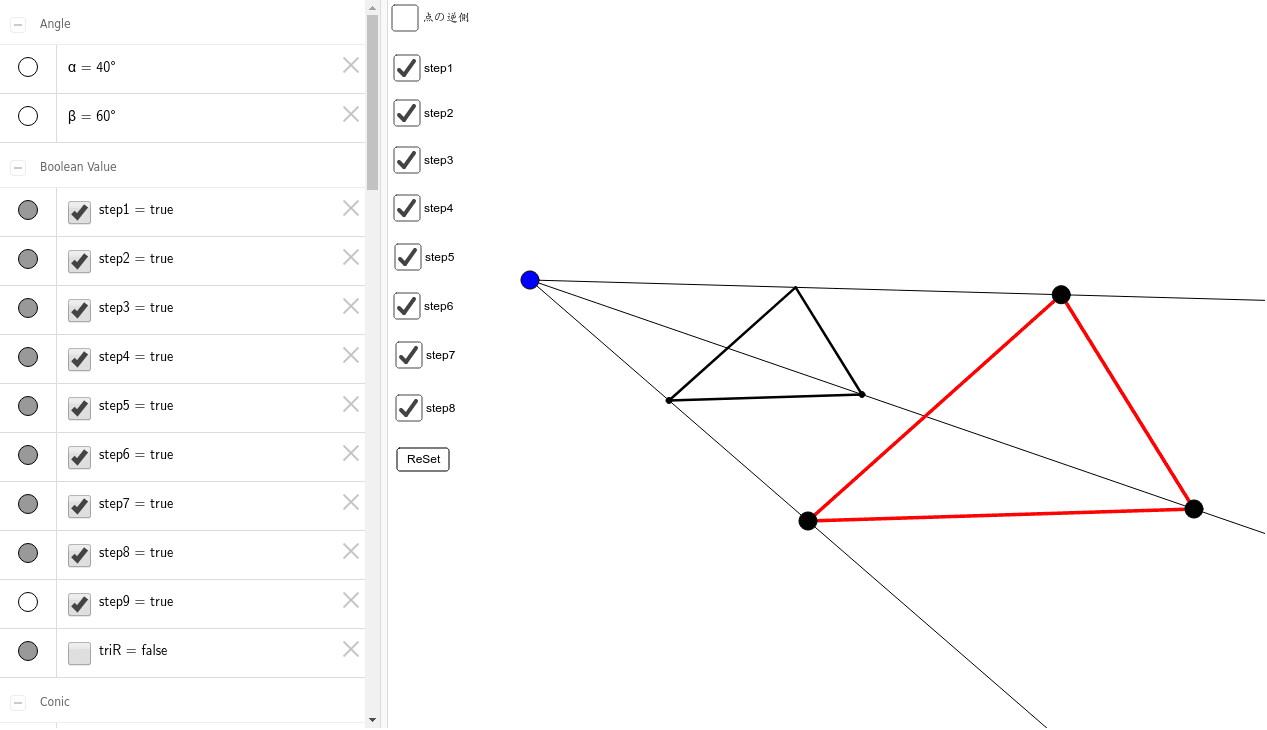



相似な図形の特徴 Geogebra
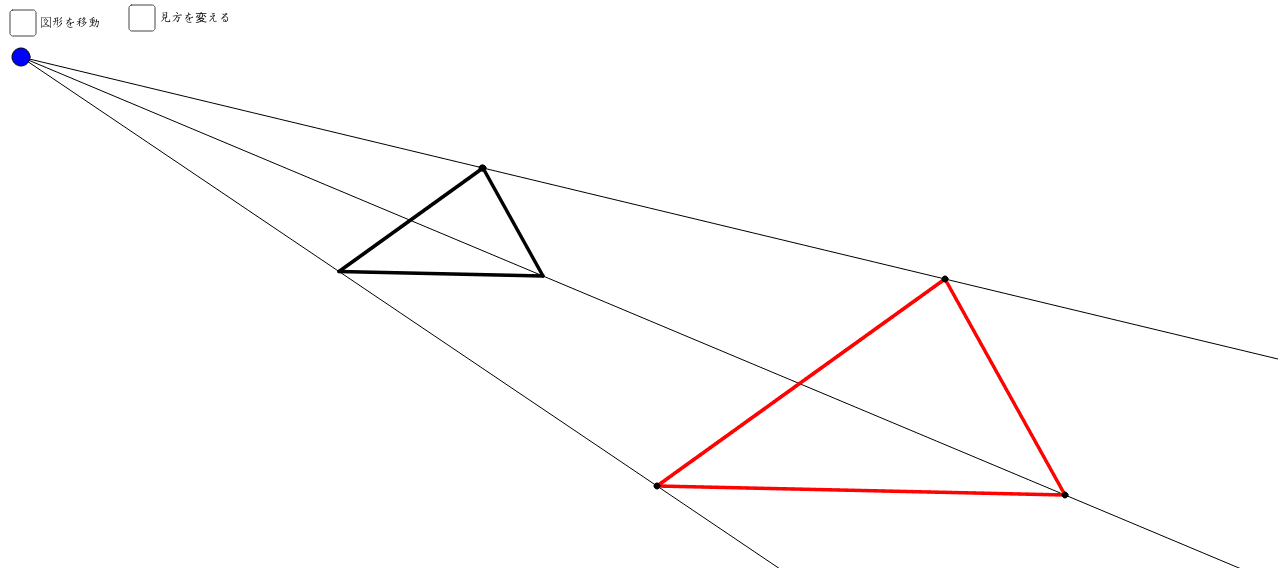



相似な図形の特徴 Geogebra




世界一わかりやすい数学問題集中3 5章 図形と相似




相似な図形 はこれでカンペキ 相似な図形のかき方8種類 算数を究める



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M3012 Pdf




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座
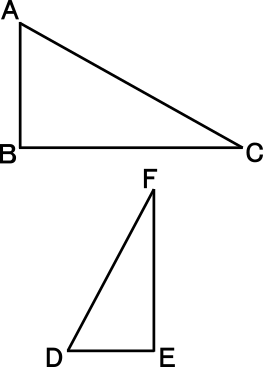



中学3年数学練習問題 相似な図形とその性質 図形の拡大と縮小
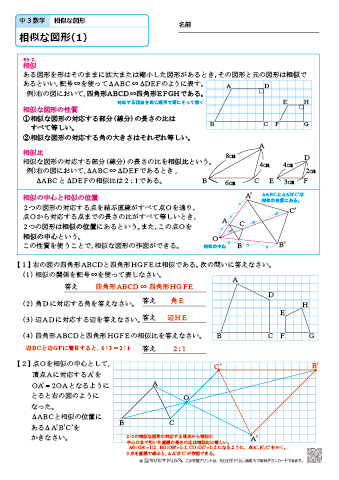



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



新潟県公立高校入試問題 相似な図形問題集




中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト



中3数学 覚えて損はない 相似な図形の性質2つ Qikeru 学びを楽しくわかりやすく



2



Studydoctor相似な図形とは 中学3年数学 Studydoctor




中3 相似な図形 中学生 数学のノート Clear



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題




Nitter



高校入試 英語 数学 図形と相似 相似の基礎



第5章3 三角形の相似 相似な図形の性質 中学生



すぐるゼミ 相似な図形の応用



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



相似な図形 計算について覚えること 苦手な数学を簡単に
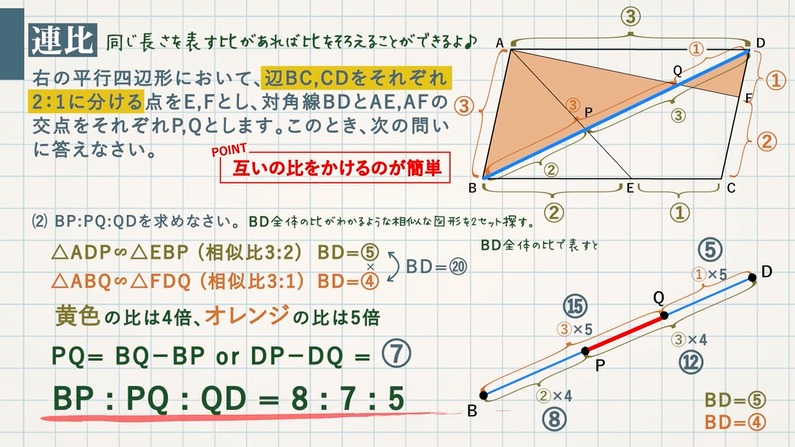



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




相似な図形と長さ 無料で使える中学学習プリント
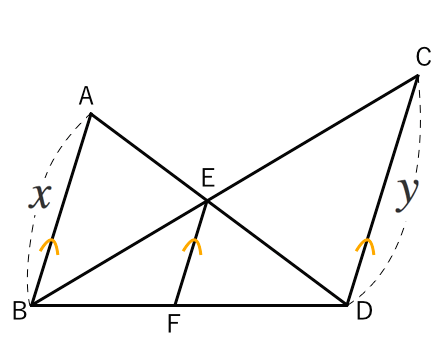



相似な図形 ピンポイント計算式 苦手な数学を簡単に



中学数学到達度テスト集中3後期 相似な図形 円 三平方の定理 図形と計量 Gakurin1346 学林舎 通販 Yahoo ショッピング




中3 数学相似まとめてみた 中学生 数学のノート Clear
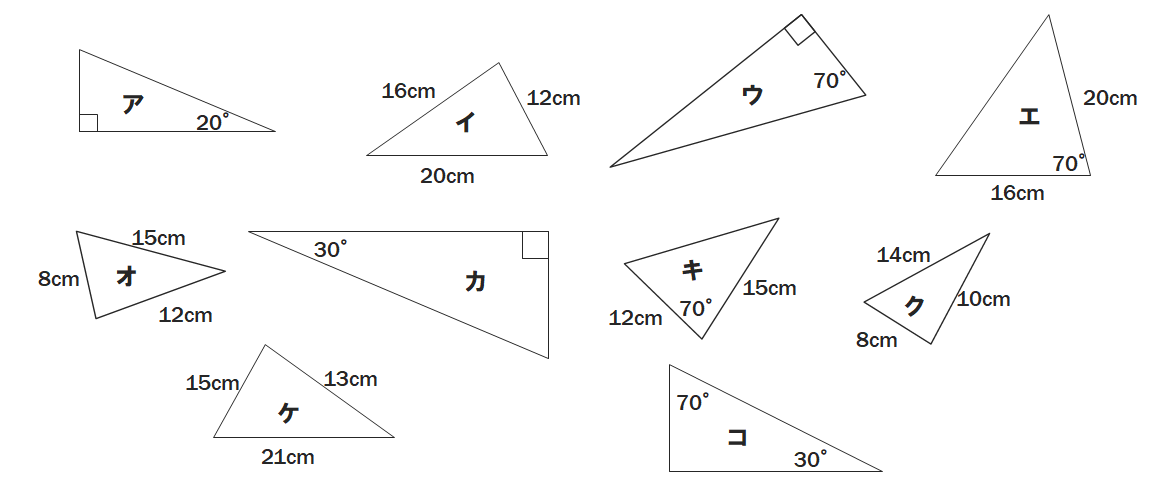



中3数学 相似な図形の線分比の定期テスト対策問題 Examee



U9j580gf8iba369ji2w Xyz P 1096



Studydoctor相似な図形や中心の作図 中3数学 Studydoctor
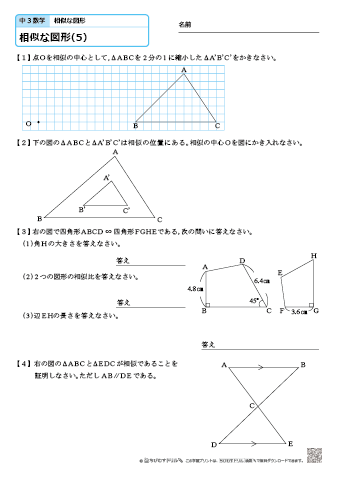



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



相似な図形 三角形の相似条件 相似比 勉強ナビゲーター
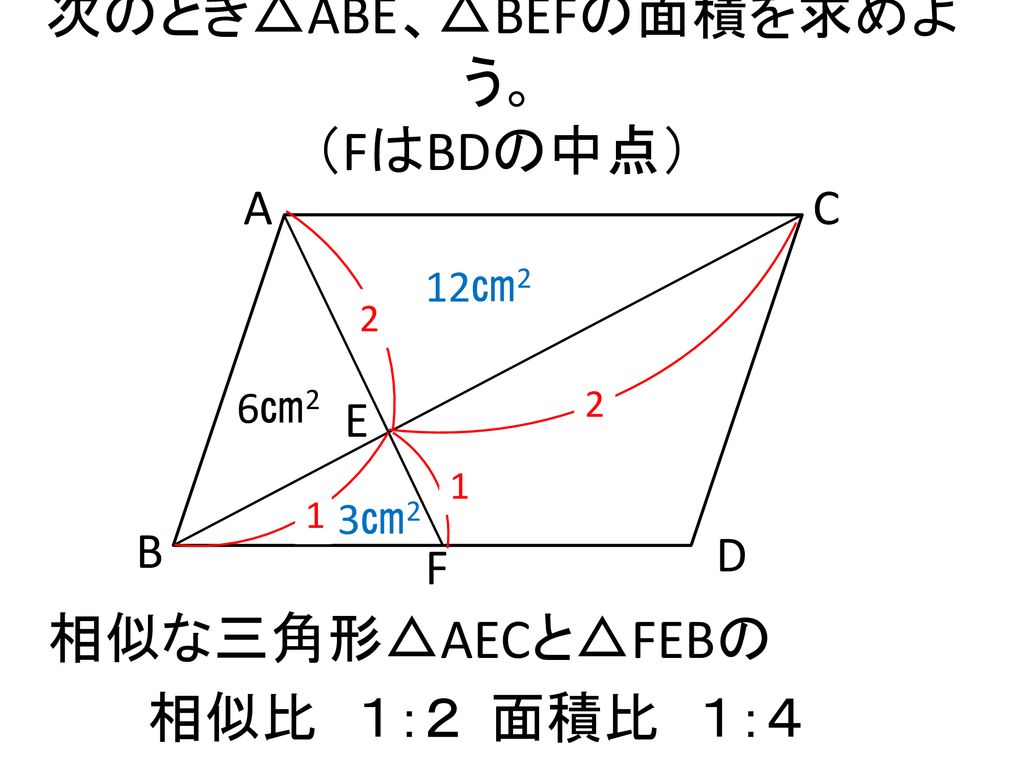



本時の目標 相似な図形の相似比と面積比の関係を理解し それを用いて相似な図形の面積を求めることができる Ppt Download




中学三年相似な図形の範囲です の問題なのですが 何故 相似比が3 2 数学 教えて Goo




相似な図形 チーム エン




相似な図形 Ict教材eboard イーボード




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明




相似な図形の面積と体積 の問題のわからないを5分で解決 映像授業のtry It トライイット
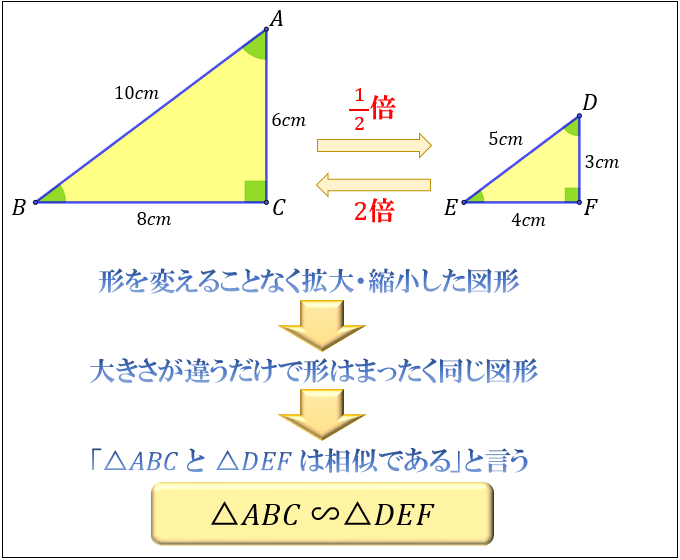



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ




相似な図形 Ict教材eboard イーボード



2




中3数学 図形と相似31 相似な図形の面積比 すべて無料 星組の中学数学講座




初等数学模索生活 相似な図形 3



1




相似な図形の比 数学i フリー教材開発コミュニティ Ftext




中学校 第3学年 数学 相似な図形 国立大学法人 大阪教育大学



Www1 Iwate School Jp Action Common Download Main Upload Id 1438




中学校 第3学年 数学 相似な図形 国立大学法人 大阪教育大学
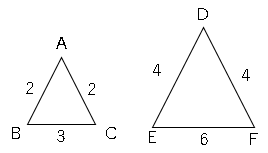



相似な図形の面積比と表面積と体積の関係 数学の要点まとめ 練習問題一覧
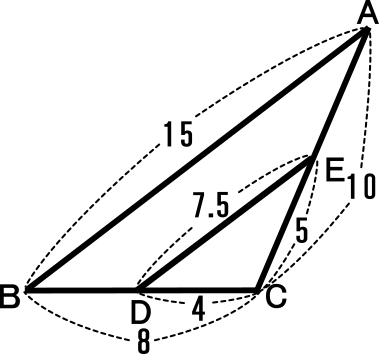



中学3年数学練習問題 三角形の相似条件と証明の問題



5章3節01 相似な図形の面積比 中村 翔




相似な図形 三角形の相似条件 中学数学 By となりがトトロ マナペディア



相似比



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
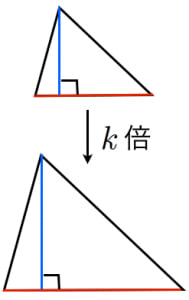



相似比と面積比 体積比の公式の証明 高校数学の美しい物語
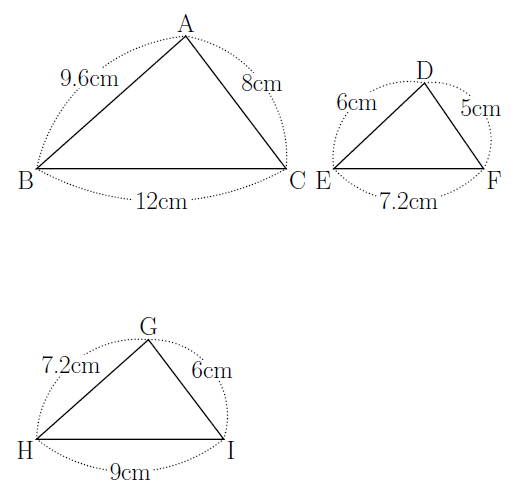



中学数学 攻略法 相似な図形の見つけ方のコツ 数樂管理人のブログ




相似な図形 Ict教材eboard イーボード
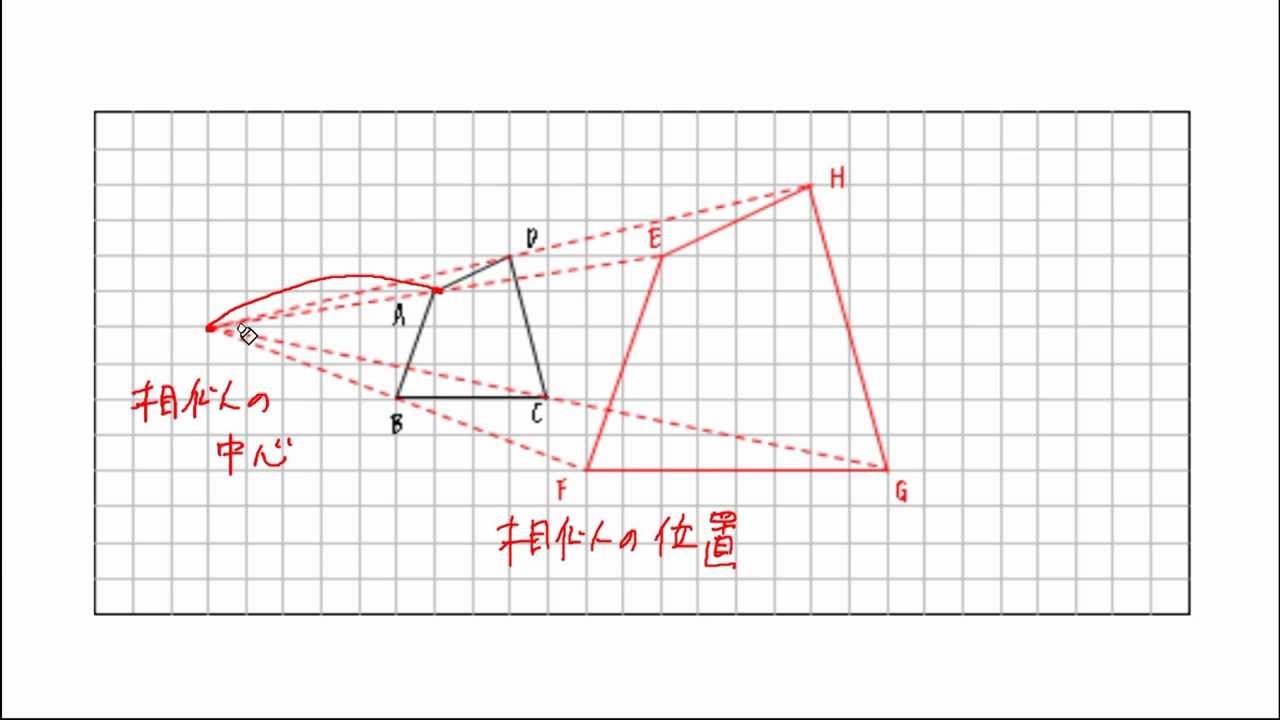



相似の中心と作図 Youtube
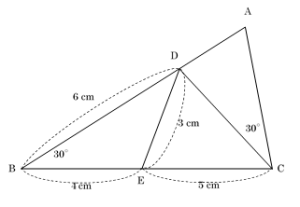



相似な図形 おやじさん ネット




相似な図形の面積比 Youtube



相似比 簡単に計算できる電卓サイト




世界一わかりやすい数学問題集中3 5章 図形と相似



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生
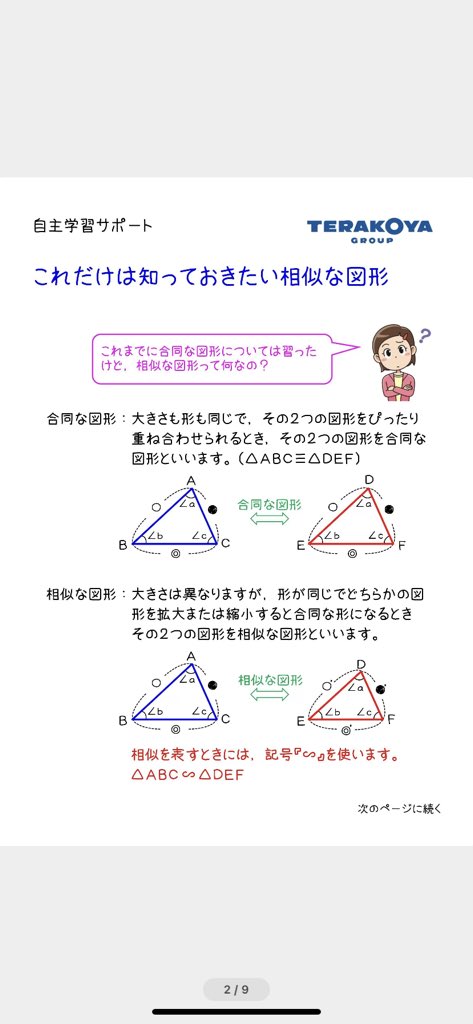



相似


